Las conclusiones a las que se arriban a partir de las actividades realizadas, se resumen en la siguiente definición:
"La función lineal es una expresión y=ax+b, donde a y b son números reales que se denominan constantes con a distinto de cero, que es la pendiente. Los términos x e y se denominan variables, x la variable independiente e y se denomina la variable dependiente. Además las rectas paralelas tienen la misma pendiente y las perpendiculares tienen pendientes invertidas con signo opuesto"
Las nuevas tecnologías nos permiten incorporar otras estrategias en el ámbito educativo. Los invitamos a utilizar el siguiente webquest para realizar una actividad con el fin de conocer la función lineal. Esta tarea consiste en realizar algunas actividades relacionadas con la función a analizar, utilizando distintos recursos como el GeoGebra y un video que permite profundizar algunas partes importantes del tema.
Nombre y Apellidos del Autor:
Idioma:
Nivel Educativo:
Area de Conocimiento:
Para la evaluación se tendrán en cuenta los siguientes criterios:
1) Trabajo en equipo, respetando las opiniones de los demás.
2) Trabajo individual, en su netbook, escribir las respuestas que considere con sus propias palabras y agregando los gráficos necesarios que acompañen su desarrollo.
3) Nivel de claridad en las ideas expresadas de forma coherente con lo visualizado.
4) Mostrar y explicar la producción a los demás grupo de compañeros.
5) Entrega en tiempo y forma de la actividad planteada.
Introducción:
En esta actividad los invitamos a trabajar el concepto de función lineal mediante su representación gráfica y algebraica, abarcando diferentes situaciones y problemas. Les proponemos el uso del programa GeoGebra (instalado en las netbooks de la secundaria), para visualizar los gráficos de las distintas funciones y sacar conclusiones desde allí. Además, se proporciona un recurso audiovisual para afianzar uno de los contenidos importantes (pendiente) dentro del concepto elegido (función lineal).
Las tareas serán variadas. Algunas serán de tipo individual. Otras, las realizará con su pequeño grupo (no más de 3). Y en la evaluación, compartirá su producción con la de los demás grupos de compañeros. Para el proceso de aprendizaje, deberá realizar las siguientes tareas:
-Tarea individual de leer los diferentes problemas que se presentan.
-Tarea con su pequeño grupo de trabajo, en la que deberán debatir formas de resolución y tratar de escribir una ecuación que represente la situación planteada.
-Tarea individual de entregar un archivo con las actividades resueltas.
_________________________________________________________________________________
Actividad 1:
Analicen la siguiente situación: Una empresa que se dedica a la reparación de electrodomésticos cobra $100 por la visita domiciliaria, más $50 por cada hora de trabajo adicional. Respondan a las siguientes consignas:
a) Planteen una ecuación o fórmula que permita calcular el dinero que debemos pagar (y) en función de las horas trabajadas (x).
b) Representen gráficamente la ecuación propuesta. Para hacerlo, utilicen el programa Geogebra instalado en sus netbooks. Utilice el comando tabla para obtener una tabla de valores para x e y.
c) Si el técnico permanece 5 horas en el domicilio, ¿cuánto se deberá abonar?
Actividad 2:
Utilizando el programa GeoGebra representen las siguientes funciones. Luego, empleando el procesador de textos contesten las preguntas que aparecen debajo:
a) y=3x+4
b) y=3(x+2)
c) 2y=6x+8
d) 9y=-3x+18
* De las rectas graficadas, ¿cuáles son paralelas a la función y=3x+1?
* De las rectas graficadas, ¿cuáles son perpendiculares a la función y=3x+1?
* Dar la fórmula y graficar otros ejemplos de rectas paralelas y perpendiculares a la función y=3x+1.
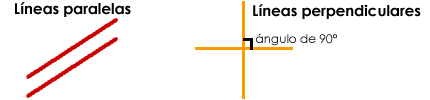
* ¿Cómo son las pendientes entre las rectas que son paralelas?
* ¿Cómo son las pendientes entre las rectas que son perpendiculares?
_________________________________________________________________________________
1) Lea en forma individual las consignas planteadas.
2) Halle con su grupo, una ecuación que represente la situación en cada problema.
3) Cuando se le pida, utilice los recursos propuestos, como el GeoGebra y el video.
4) Debatan sobre las posibles respuestas y comparen sus gráficos hechos de manera individual, para ver si coinciden o no y por qué.
5) Responda las preguntas de las consignas en forma individual, para luego entregar el archivo de trabajo.